PUBLISH IN SOME JOURNAL AND MY MAIN NICE RESULT

 I.In Forum Geometricorum Jounal

Web site Forum Geometricorum

1- Đào Thanh Oai, Volum 14, Issue 10,  A simple proof of Gibert's generalization of the Lester circle theorem

2- Đào Thanh Oai, Volum 14, Issue 18,   Two pairs of Archimedean circles in the arbelos

3- Nikolaos Dergiades, Volum 14, Issue 24, Dao's theorem on six circumcenters associated with a cyclic 

4- Telv Cohl, Volum 14, Issue 29, A Purely Synthetic Proof of Dao’s Theorem on Six Circumcenters Associated with a Cyclic Hexagon

5-Dao Thanh Oai, Equilateral triangles and Kiepert perspectors in complex numbers, 105--114. 

6- Dao Thanh Oai and Paul Yiu, Some simple constructions of equilateral triangles associated with a triangle (accepted)

7- Ngo Quang Duong, Two generalizations of the Simson line theorem (submited)

8-Dao Thanh Oai, On the Jacobi Triangle (accepted)

II. In Crux Mathematicorum

Web site Crux Mathematicorum

1- Problem 3845, Issue 5, Volum 39

2- Problem 3869, Isue 7, Volum 39
3-  Problem 3878, Isue 8, Volum 39

4-  Problem 3885, Isue 9, Volum 39
5- Problem 3894(Dao Thanh Oai and Nguyen Minh Ha), Isue 10, Volum 39

III. In Global Journal of advanced research on classical and mordern geometries (Romania)

 Web site GLOBAL JOURNAL OF ADVANCED RESEARCH ON CLASSICAL AND MODERN GEOMETRIES

1- Trần Hoàng Sơn, Volum 3, Issue 2, A SYNTHETIC PROOF OF DAO’S GENERALIZATION OF GOORMAGHTIGH’S THEOREM

2-Dao Thanh Oai-Nguyen Minh Ha, AN INTERESTING APPLICATION OF THE BRITISH FLAG THEOREM, Global Journal of Advanced Research on Classical and Modern Geometries ISSN: 2284-5569, Vol.4, (2015), Issue 1, pp.31-34

3-Nguyen Ngoc Giang, A proof of Dao's theorem (accepted)
  
IV. International jourbal of Geometry (Romania)

Web site International jourbal of Geometry

Organized by the Department of Mathematics and Computer Science, Vasile Alecsandri National College of Bacau and Vasile Alecsandri University of Bacau,

Web site International Journal of Geometry

1- Telv Cohl, Volum 3, Isue 8, DAO'S THEOREM ON CONCURRENCE OF THREE EULER LINES

2- Đào Thanh Oai, Volum 3, A SYNTHETIC PROOF OF A. MYAKISHEV'S GENERALIZATION OF VAN LAMOEN CIRCLE THEOREM AND AN APPLICATION

V. ENCYCLOPEDIA OF TRIANGLE CENTERS

Web site ENCYCLOPEDIA OF TRIANGLE CENTERS

1- X(4240) = DAO TWELVE EULER LINES POINT

2- X(5569) = CENTER OF THE DAO 6-POINT CIRCLE

3-X(5607) = CENTER OF 1st POHOATA-DAO-MOSES CIRCLE

4-X(5608) = CENTER OF 2nd POHOATA-DAO-MOSES CIRCLE

5-X(6103) = RADICAL CENTER OF THE DAO-MOSES-TELV CIRCLE, CIRCUMCIRCLE, AND NINE-POINT CIRCLE

6-X(6118) = CENTER OF 1st DAO-VECTEN CIRCLE

7-X(6119) = CENTER OF 2nd DAO-VECTEN CIRCLE

8-X(6188) = DAO (a,b,c,R) PERSPECTOR

9-DAO'S CONJUCTURE GENERALIZATION OF THE LESTER CIRCLE

VI. THE MATHEMATICAL GAZETTE

1-Dao Thanh Oai, A family of Napoleon triangles associated with the Kiepert configuration, The Mathematical Gazette, Published online: 13 March 2015

2- Nguyen Le Phuoc, Nguyen Chuong Chi, A proof of Dao generalization of the Simson line theorem (accepted)

VII-AMERICAN MATHEMATICAL MONTHLY

1-Problem 11830, The American Mathematical Monthly Vol. 122, No. 3 (March 2015), pp. 284-291 Published by: Mathematical Association of America

VIII-SOMES ANOTHER NICE RESULT

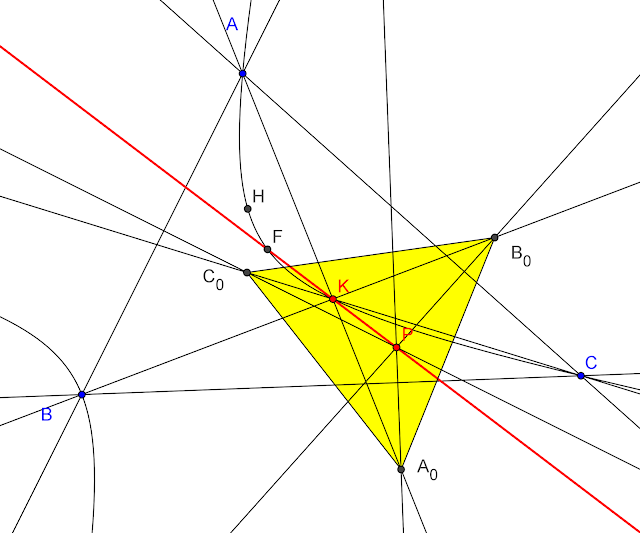
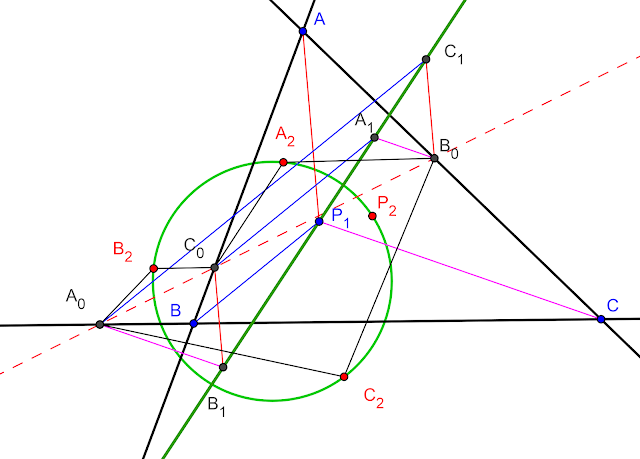
1-A generalization Gossard perspector theorem

Let $ABC$ be a triangle, Let $P_1,P_2$ be two points on the plane, the line $P_1P_2$ meets $BC, CA, AB$ at $A_0,B_0,C_0$ respectively. Let $A_1$ be a point on the plane such that $B_0A_1$ parallel to $CP_1$, $C_0A_1$ parallel to  $BP_1$. Define $B_1, C_1$ cyclically. Let $A_2$ be a point on the plane such that $B_0A_2$ parallel to $CP_2$, $C_0A_2$ parallel to  $BP_2$. Define $B_2, C_2$ cyclically. 

Problem 1: The triangle bounded by three lines  $A_1A_2,B_1B_2,C_1C_2$ homothety and congruent to $ABC$, the homothetic center $Q$ lie on $P_1P_2$

Problem 2: Newton lines of four quadrilateral $(AB,AC,A_1A_2,L)$, $(BC,BA,B_1B_2,L)$, $(CA,CB,C_1C_2,L)$, $(AB,BC,CA,L)$ also through the homothetic center in problem 1. Where if Li (i=1,2,...n) be a line, define (L1,L2,....,Ln) = Polygon bound by L1,L2,L3...,Ln

Click to see in post AoPS

2-A generalization of the Napoleon theorem associated with Kiepert hyperbola

Let ABC be a triangle, $F$ be the first (or secon) Fermat point, let $K$ be the point on the Kiepert hyperbola. Let $P$ be the point on line FK. The line through P and perpendicular to $BC$ meet $AK$ at $A_0$. Define $A_0,B_0,C_0$ cyclically. Show that $A_0B_0C_0$ is an equilateral triangle. This triangle homothety to the outer(or inner) Napoleon triangle.

Please click to see a solution in AoPS

3-A generalization Simson line theorem 1

 Let $ABC$ be a triangle, let a line $L$ through circumecenter, let a point $P$ lie on circumcircle. Let $AP,BP,CP$ meets $L$ at $A_P, B_P, C_P$. Denote A_0,B_0,C_0 are projection (mean perpendicular foot) of $A_P, B_P, C_P$ to $BC,CA,AB$ respectively. Then $A_0,B_0,C_0$ are collinear. The new line $\overline {A_0B_0C_0}$ bisects the orthocenter and $P$. When $L$ pass through $P$, this line is Simson line.

See two proof in AoPS and  Click to get another proof in yahoo discustion Advanced Plane Geometry

4. 2nd Ageneralization Simson line theorem

Let a circumconic of the triangle ABC, let Q, P be two points on the plane. Let PA,PB,PC intersect the conic at A1,B1,C1 respectively. QA1 intersects BC at A2, QB1 intersects AC at B2, QC1 intersects AB at C2. Then four points A2,B2,C2,D are colinear if only if Q lie on the conic.

See two link in AoPS: Link 1 in AoPS ; Link 2 in AoPS

See link in Geoff Smith's paper, publish in Mathematical Gazette

5-A generalization of Parry Circle

Let a rectangular circumhyperbola of ABC, let L is the isogonal conjugate line of the rectangular hyperbola. The tangent line of the hyperbola at X(4) meets L at point K. The line through K and center of the hyperbola meets the hyperbola at $F_+,F_-$.  Let  $ I_+,I_-,G$ be the isogonal conjugate of $F_+,F_-$ and $K$ respectively. Let F be the inverse point of  G with respect to the circumcircle of ABC.  Show that: $I_+,I_-,G, X(110), F$ alway lie on a circle, this circle is a generalization of Parry circle. Furthemore K alway lie on the Jerabek hyperbola.

Click to see post in AoPS

6. A generalization Steiner line and Miquel circle

Let $ABC$ be a triangle, Let $P_1$ be any point on the plane. Let a line $L$ meets $BC, CA, AB$ at $A_0,B_0,C_0$ respectively. Let $A_1$ be a point on the plane such that $B_0A_1$ parallel to $CP_1$, $C_0A_1$ parallel to $BP$. Define $B_1, C_1$ cyclically.

Generalization of the Steiner line: Then show that: $A_1, B_1, C_1, P_1$ are collinear.

A gneralization of Miquel circle: Define $A_2,B_2,C_2,P_2$ be the isogonal conjugates $A_1,B_1,C_1,P_1$ respect to $AB_0C_0, BC_0A_0, CA_0B_0$ and $ABC$ (respectively). Then show that $A_2,B_2,C_2,P_2$ lie on a circle.

http://tube.geogebra.org/material/show/id/1434055

See post and two proof in AoPS

7. A generalization specialcase of Brianchon theorem and Pascal theorem in one configuration

Let six circles $(O_1), (O_2), (O_3), (O_4), (O_5), (O_6)$. Let  $(O_i), (O_{i+1})$ cut at $A_i, A'_i$ for $i=1, 2, 3, 4, 5, $6 (Here we take modulo 6).  Let $A_1, A_2, A_3, A_4, A_5, A_6$ lie on a circle and  $A'_1, A'_2, A'_3, A'_4, A'_5, A'_6$  lie on another circle.
 
1. (A generalization of Pascal theorem) Then show that six points which they are intersection of
$(O_1)$, $(O_4)$; $(O_2)$, $(O_5)$; $(O_3)$, $(O_6)$ (if they are exist) lie on a circle.
 
2. (A generalization of Brianchon theorem) Three lines $O_1O_4$, $O_2O_6$, $O_3O_5$ are concurrent (Problem 3845, Proposed by Dao Thanh Oai, Kien Xuong, Thai Binh, Viet Nam, Crux Mathematicorum, Volum 39; Solution by Luis Gonzalez)

Applet in Geogebra website